Liczby całkowite
Liczby całkowite - to liczby naturalne oraz ich ujemne odpowiedniki, a także liczba zero:
...−4,−3,−2,−1, 0, 1, 2, 3, 4, ...
Zbiór liczb całkowitych oznaczamy symbolem Z.
Z={...−4,−3,−2,−1, 0, 1, 2, 3, 4, ...}
Liczby wymierne
Liczba wymierna - to taka liczba, którą można zapisać w postaci ułamka zwykłego, czyli w postaci ułamka:
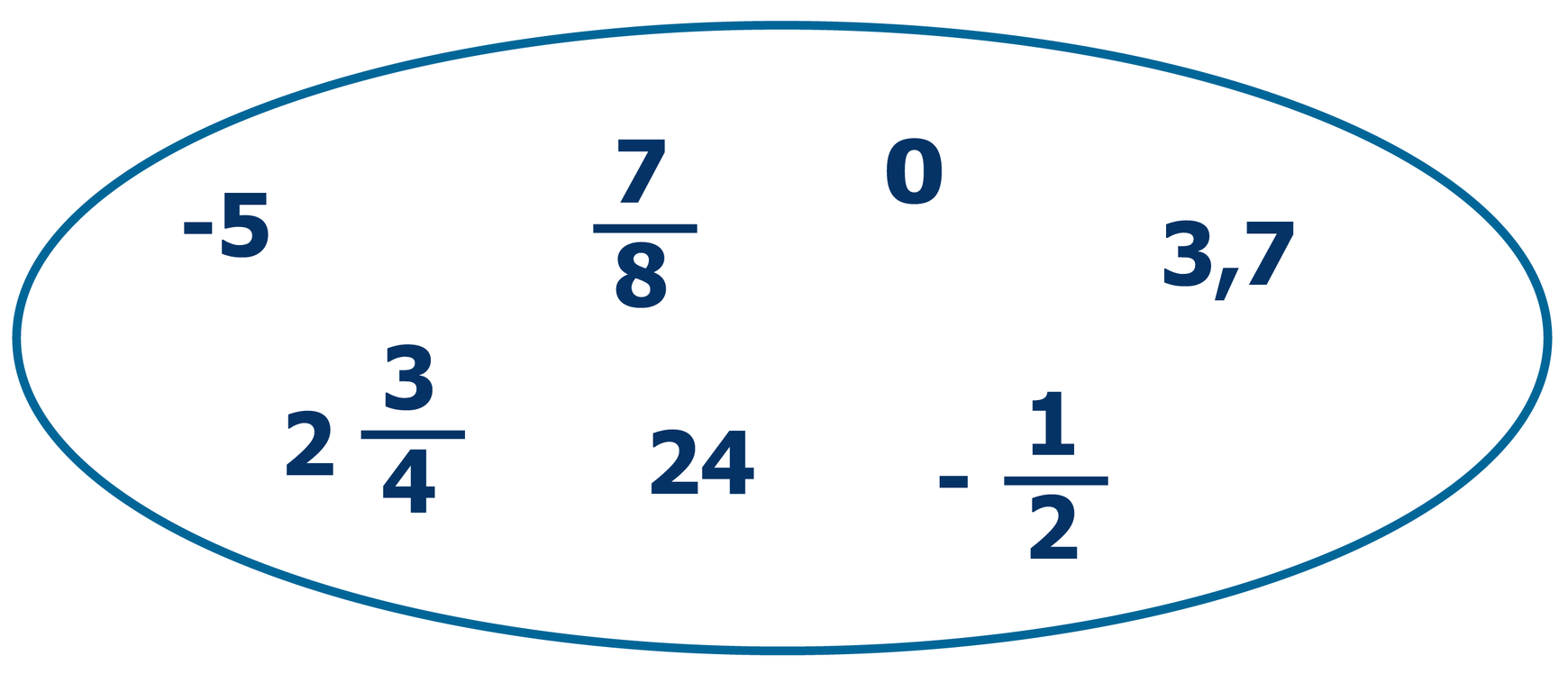
Zbiór liczb wymiernych oznaczamy symbolem Q.
Działania na liczbach całkowitych
Dodawanie i odejmowanie
Jeśli dwie są dodatnie, dodajemy je tak jak liczby naturalne.
np. 15+20=35
Jeśli dwie są ujemne (-a) i (-b), to wynikiem dodawania jest liczba -(a + b)
np. (-15)+(-20)=-35
Jeśli jedna liczba jest dodatnia (a), a druga ujemna (-b) to znaki "+" oraz "-" stojące obok siebie przyjmują znak "-"
np. 15+(-20)=15-20=-5
Mnożenie i dzielenie
Iloczyn (iloraz) nieparzystej liczby czynników ujemnych jest liczbą ujemną:
a · (-b) = -(a · b)
np. (-3)*(-5)*(-10)=-150
Iloczyn (iloraz) parzystej liczby czynników ujemnych jest liczbą dodatnią:
(-a) :(-b) = +(a · b)
np. 60 : (-2) * (-3) = 90
Działania na liczbach całkowitych
Kliknij "Kolejne zadanie", aby rozpocząć.
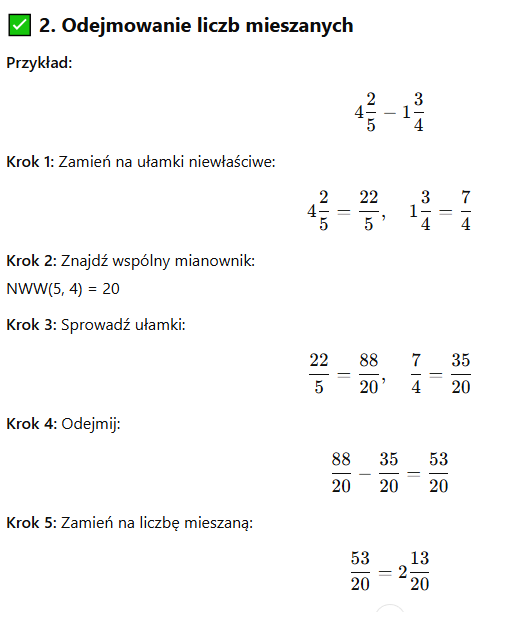
Działania na liczbach wymiernych
Przykłady: