Liczby naturalne

0,1,2,3,4,5, …. to liczby naturalne. Można je uporządkować rosnąco, wtedy dla dowolnej liczby naturalnej n następna jest liczba n+1.
Liczb naturalnych jest nieskończenie wiele.

Zbiór liczb naturalnych oznaczamy literą N.
Możemy zapisać, że: N={0,1,2,3,4,5,...}

Dzielniki liczby

Słowem dzielnik określamy liczbę
w dzieleniu, ale termin dzielnik liczby oznacza liczbę, która dzieli ją bez reszty.
Dzielnikami liczby 18 są: 1, 2, 3, 6, 9, 18, ponieważ każda z liczb dzieli 18 bez reszty.
Zapisujemy wówczas D₁₈={1, 2, 3, 6, 9, 18}

Wielokrotność liczby

Wielokrotności liczby otrzymujesz mnożąc daną liczbę przez kolejne liczby naturalne.
0 jest wielokrotnością każdej liczby naturalnej.

Liczby parzyste i nieparzyste

Liczba parzysta - to taka liczba całkowita, którą można podzielić przez 2 (bez reszty):
...-4, -2, 0, 2, 4, ...

Liczba nieparzysta - to taka liczba całkowita, której nie można podzielić przez 2 (przy dzieleniu przez 2 daje resztę 1):
...−5, −3, −1, 1, 3, 5, ...

Liczba pierwsza i złożona

Liczbę naturalną, która ma dokładnie dwa dzielniki (1 i samą siebie), nazywamy
liczbą pierwszą:

2, 3, 5, 7, 11, 13, ....

Liczba złożona ma więcej niż dwa dzielniki:
4, 6, 8, 9, 10, 12,...

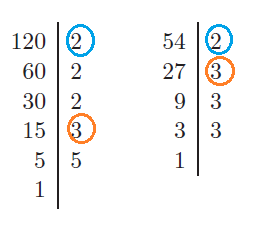
Wyznaczanie NWD (największego wspólnego dzielnika)

Korzystając z podanych obok rozkładów na czynniki pierwsze liczb 120 i 54, otrzymujemy:

NWD(120, 54) = 2 · 3 = 6

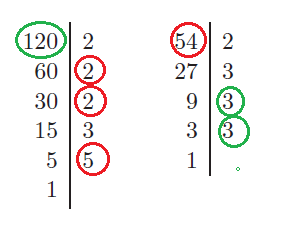
Wyznaczanie NWW (najmniejszej wspólnej wielokrotności)

Korzystając z podanych obok rozkładów na czynniki pierwsze liczb 120 i 54, otrzymujemy:

NWW(120, 54) = 54 · 2 · 2 · 5 = 1080
lub
NWW(120, 54) = 120 · 3 · 3 = 1080

Cechy podzielności liczb przez:

2, gdy ostatnią jej cyfrą jest jedna z cyfr: 0, 2, 4, 6, 8;
3, gdy suma jej cyfr jest podzielna przez 3;
4, gdy dwie ostatnie cyfry tworzą liczbę podzielną przez 4;
5, gdy ostatnią jej cyfrą jest 0 lub 5;
6, gdy jest podzielna przez 2 i przez 3;
9, gdy suma jej cyfr jest podzielna przez 9.

Aby zobaczyć rozwiń listę:

Przykład liczb podzielnych przez 2:

2, 8, 24, 720, 1569854

Przykład liczb podzielnych przez 3:

49518, ponieważ 4+9+5+1+8=27
Liczba 27 jest podzielna przez 3

Przykład liczb podzielnych przez 4:

50316, ponieważ liczba 16 jest podzielna przez 4

Przykład liczb podzielnych przez 5:

105, ponieważ jej ostatnia cyfra to 5
6910, ponieważ jej ostatnia cyfra to 0

Przykład liczb podzielnych przez 6:

324, ponieważ jest parzysta oraz suma jej cyfr 3+2+4=9 jest podzielna przez 3

Przykład liczb podzielnych przez 9:

5634, ponieważ suma jej cyfr 5+6+3+4=18 jest podzielna przez 9

Rozwiąż test

Liczby naturalne

Wybierz poziom trudności:

Kliknij "Kolejne zadanie", aby wygenerować nowe zadanie.